neka su

i

redom tocke u kojima simetrale unutarnjeg i vanjskog kuta iz vrha

, trokuta

, sijeku pravac

. ako je
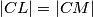
, dokazite da je
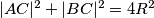
, gdje je

duljina polumjera kruznice opisane trokutu

%V0
neka su $L$ i $M$ redom tocke u kojima simetrale unutarnjeg i vanjskog kuta iz vrha $C$, trokuta $ABC$, sijeku pravac $AB$. ako je $|CL| = |CM|$, dokazite da je $|AC|^2 + |BC|^2 = 4R^2$, gdje je $R$ duljina polumjera kruznice opisane trokutu $ABC$