Neka su točke
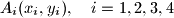
na hiperboli
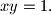
Dokažite tvrdnju: ako su sve četiri točke na istoj kružnici, onda je
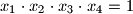
.
%V0
Neka su točke $A_i(x_i,y_i),\quad i=1, 2, 3, 4$ na hiperboli $xy=1.$ Dokažite tvrdnju: ako su sve četiri točke na istoj kružnici, onda je $x_1 \cdot x_2 \cdot x_3 \cdot x_4=1$.