Razlika recipročnih vrijednosti dvaju uzastopnih prirodnih brojeva je
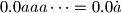
. Koje vrijednosti može poprimiti znamenka

?
%V0
Razlika recipročnih vrijednosti dvaju uzastopnih prirodnih brojeva je $0.0aaa\dots=0.0\dot{a}$. Koje vrijednosti može poprimiti znamenka $a$?