Kut pri vrhu osnog presjeka uspravnog stošca je
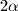
, a polumjer osnovke

. U taj stožac je upisana pravilna šesterostrana prizma čiji su svi bridovi jednake duljine (jedna osnovka prizme leži u ravnini osnovke stošca, a preostali vrhovi na plaštu stošca). Izračunaj oplošje prizme pomoću

i

.
%V0
Kut pri vrhu osnog presjeka uspravnog stošca je $2\alpha$, a polumjer osnovke $r$. U taj stožac je upisana pravilna šesterostrana prizma čiji su svi bridovi jednake duljine (jedna osnovka prizme leži u ravnini osnovke stošca, a preostali vrhovi na plaštu stošca). Izračunaj oplošje prizme pomoću $\alpha$ i $r$.