An isosceles trapezoid with bases  and
and  and altitude
and altitude  is given.
is given.
a) On the axis of symmetry of this trapezoid, find all points such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
;
b) Calculate the distance of from either base;
from either base;
c) Determine under what conditions such points actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise.
 and
and  and altitude
and altitude  is given.
is given. a) On the axis of symmetry of this trapezoid, find all points
 such that both legs of the trapezoid subtend right angles at
such that both legs of the trapezoid subtend right angles at  ;
; b) Calculate the distance of
 from either base;
from either base; c) Determine under what conditions such points
 actually exist. Discuss various cases that might arise.
actually exist. Discuss various cases that might arise. Slični zadaci
Consider a cone of revolution with an inscribed sphere tangent to the base of the cone. A cylinder is circumscribed about this sphere so that one of its bases lies in the base of the cone. let 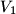 be the volume of the cone and
be the volume of the cone and 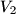 be the volume of the cylinder.
be the volume of the cylinder.
a) Prove that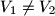 ;
;
b) Find the smallest number for which
for which 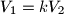 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
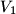 be the volume of the cone and
be the volume of the cone and 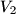 be the volume of the cylinder.
be the volume of the cylinder. a) Prove that
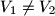 ;
; b) Find the smallest number
 for which
for which 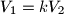 ; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.
; for this case, construct the angle subtended by a diamter of the base of the cone at the vertex of the cone.  Školjka
Školjka 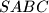 has the following property: there exist five spheres, each tangent to the edges
has the following property: there exist five spheres, each tangent to the edges 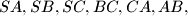 or to their extensions.
or to their extensions. 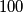 coplanar points, no three collinear, prove that at most
coplanar points, no three collinear, prove that at most 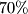 of the triangles formed by the points have all angles acute.
of the triangles formed by the points have all angles acute.  and
and 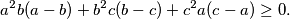
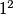 ,
, 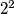 ,
, 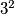 ,
,  ,
, 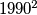 in some order.
in some order.