Prove that in the set
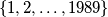
can be expressed as the disjoint union of subsets
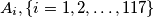
such that
i.) each
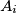
contains 17 elements
ii.) the sum of all the elements in each
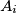
is the same.
%V0
Prove that in the set $\{1,2, \ldots, 1989\}$ can be expressed as the disjoint union of subsets $A_i, \{i = 1,2, \ldots, 117\}$ such that
i.) each $A_i$ contains 17 elements
ii.) the sum of all the elements in each $A_i$ is the same.