Slični zadaci
Given an initial integer 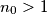 , two players,
, two players,  and
and  , choose integers
, choose integers 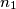 ,
, 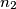 ,
, 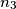 ,
,  alternately according to the following rules :
alternately according to the following rules :
I.) Knowing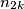 ,
,  chooses any integer
chooses any integer 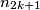 such that
such that
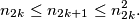
II.) Knowing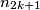 ,
,  chooses any integer
chooses any integer 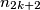 such that
such that
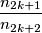
is a prime raised to a positive integer power.
Player wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 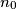 does :
does :
a.) have a winning strategy?
have a winning strategy?
b.) have a winning strategy?
have a winning strategy?
c.) Neither player have a winning strategy?
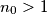 , two players,
, two players,  and
and  , choose integers
, choose integers 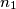 ,
, 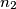 ,
, 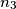 ,
,  alternately according to the following rules :
alternately according to the following rules : I.) Knowing
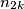 ,
,  chooses any integer
chooses any integer 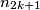 such that
such that 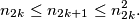
II.) Knowing
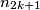 ,
,  chooses any integer
chooses any integer 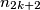 such that
such that 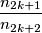
is a prime raised to a positive integer power.
Player
 wins the game by choosing the number 1990; player
wins the game by choosing the number 1990; player  wins by choosing the number 1. For which
wins by choosing the number 1. For which 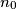 does :
does : a.)
 have a winning strategy?
have a winning strategy? b.)
 have a winning strategy?
have a winning strategy? c.) Neither player have a winning strategy?
 Školjka
Školjka 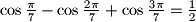
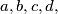 traverse, independently from each other, the set of positive real values. What are the values which the expression
traverse, independently from each other, the set of positive real values. What are the values which the expression 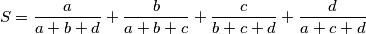 takes?
takes? 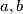 be two natural numbers. When we divide
be two natural numbers. When we divide 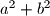 by
by 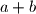 , we the the remainder
, we the the remainder  and the quotient
and the quotient 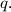 Determine all pairs
Determine all pairs 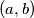 for which
for which 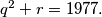
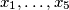 which satisfy the relations
which satisfy the relations 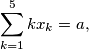
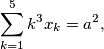
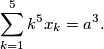
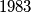 distinct positive integers, all less than or equal to
distinct positive integers, all less than or equal to 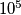 , no three of which are consecutive terms of an arithmetic progression?
, no three of which are consecutive terms of an arithmetic progression?  there exist
there exist