In a plane a set of

points (
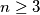
) is give. Each pair of points is connected by a segment. Let

be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length

. Prove that the number of diameters of the given set is at most

.
%V0
In a plane a set of $n$ points ($n \geq 3$) is give. Each pair of points is connected by a segment. Let $d$ be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length $d$. Prove that the number of diameters of the given set is at most $n$.