IMO Shortlist 1997 problem 24
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 For each positive integer  , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 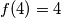 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
Prove that, for any integer we have
we have 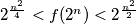 .
.
 , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 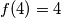 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1. Prove that, for any integer
 we have
we have 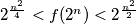 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1997
 Školjka
Školjka 
