Slični zadaci
Za sustav novčanica 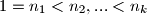 kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav
kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav 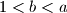 dobar ako i samo ako postoji
dobar ako i samo ako postoji  takav da je
takav da je 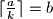 .
.
Napomena: U greedy postupku u svakom koraku vraćamo najviše moguće najvećih mogućih novčanica. Nadalje, označava najmanji cijeli broj veći od (ili jednak)
označava najmanji cijeli broj veći od (ili jednak)  .
.
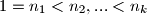 kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav
kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav 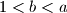 dobar ako i samo ako postoji
dobar ako i samo ako postoji  takav da je
takav da je 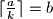 .
.Napomena: U greedy postupku u svakom koraku vraćamo najviše moguće najvećih mogućih novčanica. Nadalje,
 označava najmanji cijeli broj veći od (ili jednak)
označava najmanji cijeli broj veći od (ili jednak)  .
.  Školjka
Školjka  kosarkaskih ekipa. svaka ekipa odigrala je sa svakom drugom tocno jednu utakmicu. nerijesenih ishoda nije bilo. ako na kraju turnira
kosarkaskih ekipa. svaka ekipa odigrala je sa svakom drugom tocno jednu utakmicu. nerijesenih ishoda nije bilo. ako na kraju turnira  -ita ekipa ima
-ita ekipa ima 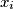 pobjeda i
pobjeda i 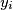 poraza
poraza 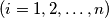 dokazite da je
dokazite da je 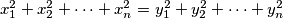
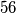 km ima
km ima  postaja
postaja  ,
, 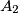 , ...,
, ..., 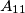 . Udaljenosti oblika
. Udaljenosti oblika 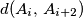 , (
, (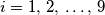 ) nisu veće od
) nisu veće od  km, a udaljenosti oblika
km, a udaljenosti oblika 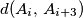 , (
, (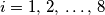 ) nisu manje od
) nisu manje od  km. Kolika je udaljenost
km. Kolika je udaljenost 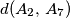 ?
?  nadite rjesenja jednadbe
nadite rjesenja jednadbe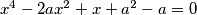
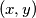 za koje vrijedi
za koje vrijedi 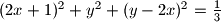 .
. 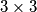 treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude
treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude 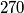 . Na koliko je načina to moguće napraviti?
. Na koliko je načina to moguće napraviti?