Slični zadaci
Let  be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 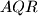 ,
, 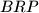 ,
, 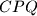 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
.
Alternative formulation: Let be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that
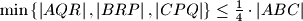 ,
,
where the abbreviation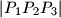 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 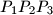 .
.
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points in the interiors of the sides
be three points in the interiors of the sides  ,
,  ,
,  of this triangle. Prove that the area of at least one of the three triangles
of this triangle. Prove that the area of at least one of the three triangles 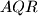 ,
, 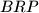 ,
, 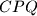 is less than or equal to one quarter of the area of triangle
is less than or equal to one quarter of the area of triangle  .
. Alternative formulation: Let
 be a triangle, and let
be a triangle, and let  ,
,  ,
,  be three points on the segments
be three points on the segments  ,
,  ,
,  , respectively. Prove that
, respectively. Prove that 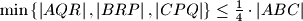 ,
, where the abbreviation
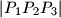 denotes the (non-directed) area of an arbitrary triangle
denotes the (non-directed) area of an arbitrary triangle 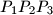 .
. We consider a prism which has the upper and inferior basis the pentagons: 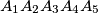 and
and 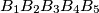 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 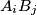 with
with 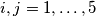 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
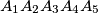 and
and 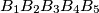 . Each of the sides of the two pentagons and the segments
. Each of the sides of the two pentagons and the segments 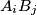 with
with 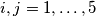 is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.
is colored in red or blue. In every triangle which has all sides colored there exists one red side and one blue side. Prove that all the 10 sides of the two basis are colored in the same color.  Školjka
Školjka  be the lengths of the sides of a triangle, and
be the lengths of the sides of a triangle, and 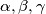 respectively, the angles opposite these sides. Prove that if
respectively, the angles opposite these sides. Prove that if 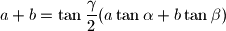 the triangle is isosceles.
the triangle is isosceles.  is
is 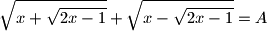 given
given 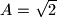 ;
; 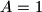 ;
; 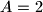 ,
,  ,
,  ,
,  be the sides of a triangle, and
be the sides of a triangle, and  its area. Prove:
its area. Prove: 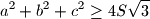
 in the plane of the triangle
in the plane of the triangle 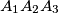 . Define
. Define 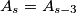 for all
for all 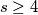 . Construct a set of points
. Construct a set of points 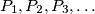 such that
such that 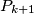 is the image of
is the image of 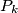 under a rotation center
under a rotation center 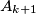 through an angle
through an angle 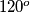 clockwise for
clockwise for 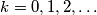 . Prove that if
. Prove that if 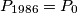 , then the triangle
, then the triangle  points in the Euclidean plane such that the distance between each pair of points is irrational and each three points determine a non-degenerate triangle with rational area? (IMO Problem 5)
points in the Euclidean plane such that the distance between each pair of points is irrational and each three points determine a non-degenerate triangle with rational area? (IMO Problem 5)