In the plane a point

is and a sequence of points
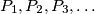
are given. The distances
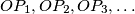
are
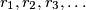
Let
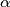
satisfies
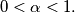
Suppose that for every

the distance from the point
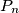
to any other point of the sequence is
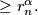
Determine the exponent
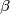
, as large as possible such that for some

independent of

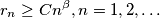
%V0
In the plane a point $O$ is and a sequence of points $P_1, P_2, P_3, \ldots$ are given. The distances $OP_1, OP_2, OP_3, \ldots$ are $r_1, r_2, r_3, \ldots$ Let $\alpha$ satisfies $0 < \alpha < 1.$ Suppose that for every $n$ the distance from the point $P_n$ to any other point of the sequence is $\geq r^{\alpha}_n.$ Determine the exponent $\beta$, as large as possible such that for some $C$ independent of $n$
$$r_n \geq Cn^{\beta}, n = 1,2, \ldots$$