Suppose
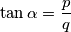
, where
and
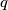
are integers and
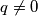
. Prove that the number
for which
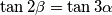
is rational only when
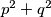
is the square of an integer.
%V0
Suppose $\tan \alpha = \dfrac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Prove that the number $\tan \beta$ for which $\tan {2 \beta} = \tan {3 \alpha}$ is rational only when $p^2 + q^2$ is the square of an integer.
Školjka