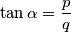
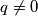
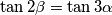
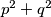
Suppose , where and are integers and . Prove that the number for which is rational only when is the square of an integer.
%V0
Suppose $\tan \alpha = \dfrac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$. Prove that the number $\tan \beta$ for which $\tan {2 \beta} = \tan {3 \alpha}$ is rational only when $p^2 + q^2$ is the square of an integer.
Izvor: Međunarodna matematička olimpijada, shortlist 1967
Školjka 
, where 
and 
are integers and 
. Prove that the number 
for which 
is rational only when 
is the square of an integer.