Zadan je trokut

s visinama
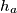
,
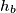
,
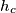
. Sjecišta simetrala kutova s nasuprotnim stranicama označimo s

,

,

, a udaljenosti točaka

,

,

od pravaca

,

,

redom sa
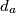
,
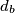
,
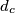
. Dokažite nejednakost
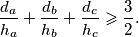
%V0
Zadan je trokut $ABC$ s visinama $h_a$, $h_b$, $h_c$. Sjecišta simetrala kutova s nasuprotnim stranicama označimo s $D$, $E$, $F$, a udaljenosti točaka $D$, $E$, $F$ od pravaca $AB$, $BC$, $CA$ redom sa $d_a$, $d_b$, $d_c$. Dokažite nejednakost $$\frac{d_a}{h_a} + \frac{d_b}{h_b} + \frac{d_c}{h_c} \geqslant \frac32 \text{.}$$