Let
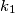
and
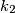
be two circles with centers
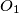
and
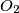
and equal radius

such that
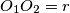
. Let

and

be two points lying on the circle
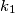
and being symmetric to each other with respect to the line
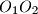
. Let

be an arbitrary point on
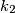
. Prove that
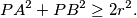
%V0
Let $k_1$ and $k_2$ be two circles with centers $O_1$ and $O_2$ and equal radius $r$ such that $O_1O_2 = r$. Let $A$ and $B$ be two points lying on the circle $k_1$ and being symmetric to each other with respect to the line $O_1O_2$. Let $P$ be an arbitrary point on $k_2$. Prove that
$$PA^2 + PB^2 \geq 2r^2.$$