Slični zadaci
The square  has to be decomposed into
has to be decomposed into  triangles (which are not overlapping) and which have all angles acute. Find the smallest integer
triangles (which are not overlapping) and which have all angles acute. Find the smallest integer  for which there exist a solution of that problem and for such
for which there exist a solution of that problem and for such  construct at least one decomposition. Answer whether it is possible to ask moreover that (at least) one of these triangles has the perimeter less than an arbitrarily given positive number.
construct at least one decomposition. Answer whether it is possible to ask moreover that (at least) one of these triangles has the perimeter less than an arbitrarily given positive number.
 has to be decomposed into
has to be decomposed into  triangles (which are not overlapping) and which have all angles acute. Find the smallest integer
triangles (which are not overlapping) and which have all angles acute. Find the smallest integer  for which there exist a solution of that problem and for such
for which there exist a solution of that problem and for such  construct at least one decomposition. Answer whether it is possible to ask moreover that (at least) one of these triangles has the perimeter less than an arbitrarily given positive number.
construct at least one decomposition. Answer whether it is possible to ask moreover that (at least) one of these triangles has the perimeter less than an arbitrarily given positive number.  Školjka
Školjka  ,
,  ,
,  satisfy the equality
satisfy the equality 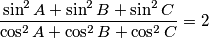
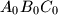 and
and 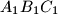 are acute-angled triangles. Describe, and prove, how to construct the triangle
are acute-angled triangles. Describe, and prove, how to construct the triangle  with the largest possible area which is circumscribed about
with the largest possible area which is circumscribed about  contains
contains 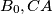 contains
contains 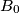 , and
, and  contains
contains 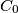 ) and similar to
) and similar to 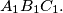
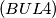 Let
Let  be the point inside the right-angled triangle
be the point inside the right-angled triangle 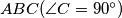 such that
such that 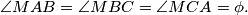 Let
Let 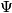 be the acute angle between the medians of
be the acute angle between the medians of  and
and 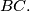 Prove that
Prove that 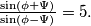
 are in the sides
are in the sides 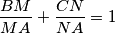 , then prove that the centroid of
, then prove that the centroid of  .
.  Six points
Six points 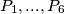 are given in
are given in 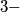 dimensional space such that no four of them lie in the same plane. Each of the line segments
dimensional space such that no four of them lie in the same plane. Each of the line segments 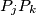 is colored black or white. Prove that there exists one triangle
is colored black or white. Prove that there exists one triangle 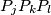 whose edges are of the same color.
whose edges are of the same color. 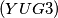 Let four points
Let four points 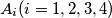 in the plane determine four triangles. In each of these triangles we choose the smallest angle. The sum of these angles is denoted by
in the plane determine four triangles. In each of these triangles we choose the smallest angle. The sum of these angles is denoted by 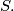 What is the exact placement of the points
What is the exact placement of the points 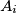 if
if 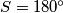 ?
?