On the circle with center 0 and radius 1 the point
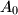
is fixed and points
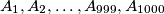
are distributed in such a way that the angle
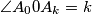
(in radians). Cut the circle at points
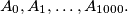
How many arcs with different lengths are obtained. ?
%V0
On the circle with center 0 and radius 1 the point $A_0$ is fixed and points $A_1, A_2, \ldots, A_{999}, A_{1000}$ are distributed in such a way that the angle $\angle A_00A_k = k$ (in radians). Cut the circle at points $A_0, A_1, \ldots, A_{1000}.$ How many arcs with different lengths are obtained. ?