Neka je

prirodan broj. Dano je

trojki cijelih brojeva
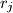
,
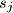
,
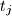
, za
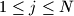
, takvih da je barem jedan od njih neparan. Pokažite da postoje cijeli brojevi

,

,

takvi da je
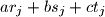
neparan, za barem
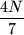
različitih indeksa

.
%V0
Neka je $N$ prirodan broj. Dano je $N$ trojki cijelih brojeva $r_j$, $s_j$, $t_j$, za $1 \leq j \leq N$, takvih da je barem jedan od njih neparan. Pokažite da postoje cijeli brojevi $a$, $b$, $c$ takvi da je $ar_j + bs_j + ct_j$ neparan, za barem $\dfrac{4N}{7}$ različitih indeksa $j$.