A convex quadrilateral

with sides
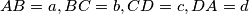
and angles
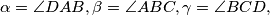
and
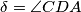
is given. Let
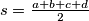
and

be the area of the quadrilateral. Prove that
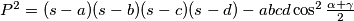
%V0
$(CZS 5)$ A convex quadrilateral $ABCD$ with sides $AB = a, BC = b, CD = c, DA = d$ and angles $\alpha = \angle DAB, \beta = \angle ABC, \gamma = \angle BCD,$ and $\delta = \angle CDA$ is given. Let $s = \frac{a + b + c +d}{2}$ and $P$ be the area of the quadrilateral. Prove that $P^2 = (s - a)(s - b)(s - c)(s - d) - abcd \cos^2\frac{\alpha +\gamma}{2}$