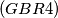
The segment

perpendicularly bisects

at

. Show that, subject to restrictions, there is a right circular cone whose axis passes through

and on whose surface lie the points
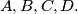
What are the restrictions?
%V0
$(GBR 4)$ The segment $AB$ perpendicularly bisects $CD$ at $X$. Show that, subject to restrictions, there is a right circular cone whose axis passes through $X$ and on whose surface lie the points $A,B,C,D.$ What are the restrictions?