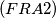
Let

be an integer that is not divisible by any square greater than
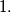
Denote by
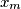
the last digit of the number
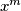
in the number system with base

For which integers

is it possible for
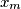
to be

? Prove that the sequence
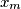
is periodic with period

independent of

For which

do we have
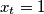
. Prove that if

and

are relatively prime, then
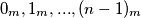
are different numbers. Find the minimal period

in terms of

. If n does not meet the given condition, prove that it is possible to have
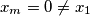
and that the sequence is periodic starting only from some number
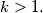
%V0
$(FRA 2)$ Let $n$ be an integer that is not divisible by any square greater than $1.$ Denote by $x_m$ the last digit of the number $x^m$ in the number system with base $n.$ For which integers $x$ is it possible for $x_m$ to be $0$? Prove that the sequence $x_m$ is periodic with period $t$ independent of $x.$ For which $x$ do we have $x_t = 1$. Prove that if $m$ and $x$ are relatively prime, then $0_m, 1_m, . . . , (n-1)_m$ are different numbers. Find the minimal period $t$ in terms of $n$. If n does not meet the given condition, prove that it is possible to have $x_m = 0 \neq x_1$ and that the sequence is periodic starting only from some number $k > 1.$
 Let
Let  be an integer that is not divisible by any square greater than
be an integer that is not divisible by any square greater than  Denote by
Denote by 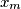 the last digit of the number
the last digit of the number 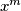 in the number system with base
in the number system with base  For which integers
For which integers  is it possible for
is it possible for 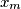 to be
to be  ? Prove that the sequence
? Prove that the sequence 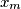 is periodic with period
is periodic with period  independent of
independent of  For which
For which  do we have
do we have 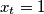 . Prove that if
. Prove that if  and
and  are relatively prime, then
are relatively prime, then 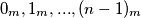 are different numbers. Find the minimal period
are different numbers. Find the minimal period  in terms of
in terms of  . If n does not meet the given condition, prove that it is possible to have
. If n does not meet the given condition, prove that it is possible to have 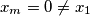 and that the sequence is periodic starting only from some number
and that the sequence is periodic starting only from some number 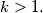
 Školjka
Školjka 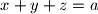
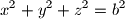
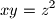 where
where  and
and  are constants. Give the conditions that
are constants. Give the conditions that  are distinct positive numbers.
are distinct positive numbers.  of the system
of the system 



 where
where  is a parameter.
is a parameter. 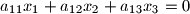
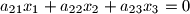
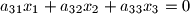 with unknowns
with unknowns 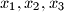 . The coefficients satisfy the conditions:
. The coefficients satisfy the conditions: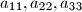 are positive numbers;
are positive numbers;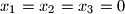 .
. 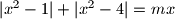 as a function of the parameter
as a function of the parameter 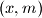 of integers satisfy this equation ?
of integers satisfy this equation ? 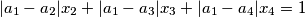
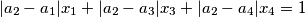
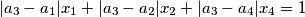
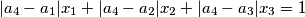 where
where 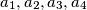 are four different real numbers.
are four different real numbers. 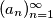 be a sequence of integers with
be a sequence of integers with 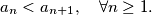 For all quadruple
For all quadruple 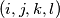 of indices such that
of indices such that 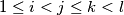 and
and 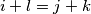 we have the inequality
we have the inequality 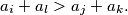 Determine the least possible value of
Determine the least possible value of 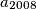 .
.