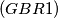 The polynomial
The polynomial 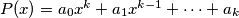 , where
, where 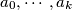 are integers, is said to be divisible by an integer
are integers, is said to be divisible by an integer  if
if  is a multiple of
is a multiple of  for every integral value of
for every integral value of  . Show that if
. Show that if  is divisible by
is divisible by  , then
, then 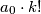 is a multiple of
is a multiple of  . Also prove that if
. Also prove that if 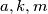 are positive integers such that
are positive integers such that 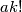 is a multiple of
is a multiple of  , then a polynomial
, then a polynomial  with leading term
with leading term 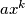 can be found that is divisible by
can be found that is divisible by 
 Školjka
Školjka  Let
Let  and
and  be arbitrary integers. Prove that if
be arbitrary integers. Prove that if  is an integer not divisible by
is an integer not divisible by  , then
, then 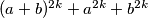 is divisible by
is divisible by 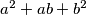
 Let
Let  and
and  be two prime numbers greater than
be two prime numbers greater than  Prove that if their difference is
Prove that if their difference is 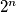 , then for any two integers
, then for any two integers 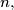 the number
the number 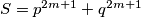 is divisible by
is divisible by 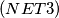 Let
Let 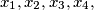 and
and 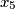 be positive integers satisfying
be positive integers satisfying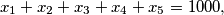
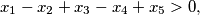
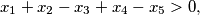
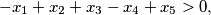
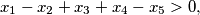
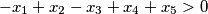
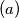 Find the maximum of
Find the maximum of 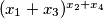
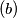 In how many different ways can we choose
In how many different ways can we choose 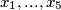 to obtain the desired maximum?
to obtain the desired maximum? 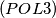 Given a polynomial
Given a polynomial 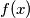 with integer coefficients whose value is divisible by
with integer coefficients whose value is divisible by 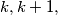 and
and 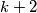 . Prove that
. Prove that 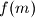 is divisible by
is divisible by 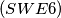 Prove that there are infinitely many positive integers that cannot be expressed as the sum of squares of three positive integers.
Prove that there are infinitely many positive integers that cannot be expressed as the sum of squares of three positive integers.