Given
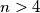
points in the plane, no three collinear. Prove that there are at least
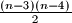
convex quadrilaterals with vertices amongst the
points.
%V0
Given $n>4$ points in the plane, no three collinear. Prove that there are at least $(n-3)(n-4)\over2$ convex quadrilaterals with vertices amongst the $n$ points.
Školjka