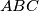
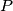
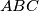
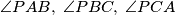
Let be a triangle and an interior point of . Show that at least one of the angles is less than or equal to .
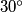
%V0
Let $\,ABC\,$ be a triangle and $\,P\,$ an interior point of $\,ABC\,$. Show that at least one of the angles $\,\angle PAB,\;\angle PBC,\;\angle PCA\,$ is less than or equal to $30^{\circ }$.
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
be a triangle and 
an interior point of 
is less than or equal to 
.