Slični zadaci
An arbitrary point  is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 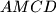 and
and 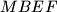 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 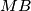 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 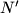 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 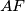 and
and  .
.
a) Prove that and
and 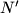 coincide;
coincide;
b) Prove that the straight lines pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
;
c) Find the locus of the midpoints of the segments as
as  varies between
varies between  and
and  .
.
 is selected in the interior of the segment
is selected in the interior of the segment  . The square
. The square 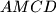 and
and 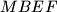 are constructed on the same side of
are constructed on the same side of  , with segments
, with segments  and
and 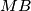 as their respective bases. The circles circumscribed about these squares, with centers
as their respective bases. The circles circumscribed about these squares, with centers  and
and  , intersect at
, intersect at  and also at another point
and also at another point  . Let
. Let 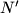 denote the point of intersection of the straight lines
denote the point of intersection of the straight lines 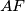 and
and  .
. a) Prove that
 and
and 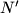 coincide;
coincide; b) Prove that the straight lines
 pass through a fixed point
pass through a fixed point  independent of the choice of
independent of the choice of  ;
; c) Find the locus of the midpoints of the segments
 as
as  varies between
varies between  and
and  .
. It is known that 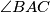 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 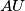 at
at  and
and  , respectively. The lines
, respectively. The lines 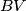 and
and 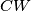 meet at
meet at  .
.
Show that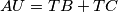 .
.
Alternative formulation:
Four different points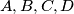 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that:
(a) The perpendicular bisectors of and
and  meet the line
meet the line  at certain points
at certain points  and
and 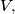 respectively, and that the lines
respectively, and that the lines 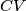 and
and 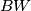 meet at a certain point
meet at a certain point 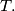
(b) The length of one of the line segments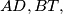 and
and 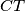 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.
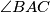 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 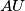 at
at  and
and  , respectively. The lines
, respectively. The lines 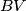 and
and 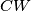 meet at
meet at  .
. Show that
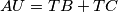 .
. Alternative formulation:
Four different points
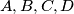 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that: (a) The perpendicular bisectors of
 and
and  meet the line
meet the line  at certain points
at certain points  and
and 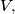 respectively, and that the lines
respectively, and that the lines 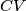 and
and 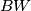 meet at a certain point
meet at a certain point 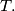
(b) The length of one of the line segments
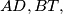 and
and 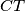 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.  Školjka
Školjka  is the foot of the perpendicular from
is the foot of the perpendicular from 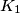 is the incircle of
is the incircle of 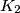 touches
touches 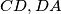 and the semicircle, the circle
and the semicircle, the circle 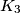 touches
touches 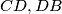 and the semicircle. Prove that
and the semicircle. Prove that 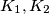 and
and  such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.
such that the median drawn to the hypotenuse is the geometric mean of the two legs of the triangle.  . The point
. The point  (with
(with 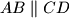 ) in which a circle can be inscribed, and with vertices
) in which a circle can be inscribed, and with vertices  there are given three distinct points
there are given three distinct points  . Construct (using only a straightedge and a compass) a fourth point
. Construct (using only a straightedge and a compass) a fourth point  being tangent to the circle on diameter
being tangent to the circle on diameter