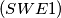
Six points
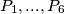
are given in
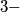
dimensional space such that no four of them lie in the same plane. Each of the line segments
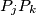
is colored black or white. Prove that there exists one triangle
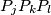
whose edges are of the same color.
%V0
$(SWE 1)$ Six points $P_1, . . . , P_6$ are given in $3-$dimensional space such that no four of them lie in the same plane. Each of the line segments $P_jP_k$ is colored black or white. Prove that there exists one triangle $P_jP_kP_l$ whose edges are of the same color.