Slični zadaci
Let  be a point inside a regular tetrahedron
be a point inside a regular tetrahedron  of unit volume. The four planes passing through
of unit volume. The four planes passing through  and parallel to the faces of
and parallel to the faces of  partition
partition  into 14 pieces. Let
into 14 pieces. Let 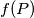 be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for
be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for 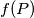 as
as  varies over
varies over 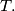
 be a point inside a regular tetrahedron
be a point inside a regular tetrahedron  of unit volume. The four planes passing through
of unit volume. The four planes passing through  and parallel to the faces of
and parallel to the faces of  partition
partition  into 14 pieces. Let
into 14 pieces. Let 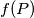 be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for
be the joint volume of those pieces that are neither a tetrahedron nor a parallelepiped (i.e., pieces adjacent to an edge but not to a vertex). Find the exact bounds for 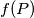 as
as  varies over
varies over 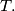
 Školjka
Školjka  be an interior point of the tetrahedron
be an interior point of the tetrahedron  . Prove that
. Prove that 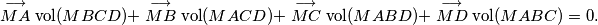
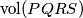 denotes the volume of the tetrahedron
denotes the volume of the tetrahedron 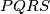 ).
).  , corresponds the point
, corresponds the point 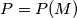 which is the intersection of two lines
which is the intersection of two lines 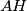 and
and 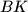 , drawn from
, drawn from  orthogonally to
orthogonally to 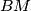 and from
and from  orthogonally to
orthogonally to  . What is the locus of
. What is the locus of  has volume at most
has volume at most 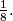
 such that there are at least three different curves on the surface joining
such that there are at least three different curves on the surface joining 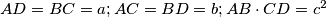 . Let
. Let 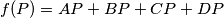 , where
, where 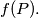
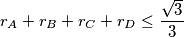
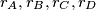 are the inradii of the faces, equality holding only if
are the inradii of the faces, equality holding only if