Let
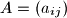
, where
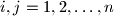
, be a square matrix with all
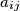
non-negative integers. For each
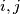
such that
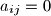
, the sum of the elements in the

th row and the

th column is at least

. Prove that the sum of all the elements in the matrix is at least
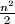
.
%V0
Let $A = (a_{ij})$, where $i,j = 1,2,\ldots,n$, be a square matrix with all $a_{ij}$ non-negative integers. For each $i,j$ such that $a_{ij} = 0$, the sum of the elements in the $i$th row and the $j$th column is at least $n$. Prove that the sum of all the elements in the matrix is at least $\frac {n^2}{2}$.