We are given
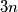
points
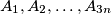
in the plane, no three of them collinear. Prove that one can construct

disjoint triangles with vertices at the points
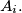
%V0
We are given $3n$ points $A_1,A_2, \ldots , A_{3n}$ in the plane, no three of them collinear. Prove that one can construct $n$ disjoint triangles with vertices at the points $A_i.$