Let 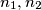 be positive integers. Consider in a plane
be positive integers. Consider in a plane  two disjoint sets of points
two disjoint sets of points 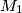 and
and 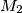 consisting of
consisting of 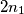 and
and 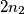 points, respectively, and such that no three points of the union
points, respectively, and such that no three points of the union 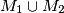 are collinear. Prove that there exists a straightline
are collinear. Prove that there exists a straightline 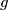 with the following property: Each of the two half-planes determined by
with the following property: Each of the two half-planes determined by 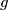 on
on  (
(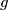 not being included in either) contains exactly half of the points of
not being included in either) contains exactly half of the points of 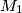 and exactly half of the points of
and exactly half of the points of 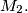
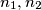 be positive integers. Consider in a plane
be positive integers. Consider in a plane  two disjoint sets of points
two disjoint sets of points 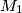 and
and 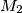 consisting of
consisting of 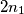 and
and 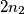 points, respectively, and such that no three points of the union
points, respectively, and such that no three points of the union  are collinear. Prove that there exists a straightline
are collinear. Prove that there exists a straightline 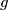 with the following property: Each of the two half-planes determined by
with the following property: Each of the two half-planes determined by 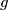 on
on  (
(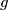 not being included in either) contains exactly half of the points of
not being included in either) contains exactly half of the points of 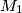 and exactly half of the points of
and exactly half of the points of 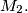
 Školjka
Školjka