Slični zadaci
Three players 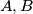 and
and  play a game with three cards and on each of these
play a game with three cards and on each of these  cards it is written a positive integer, all
cards it is written a positive integer, all  numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number
numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number 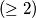 of games we find out that A has
of games we find out that A has 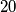 points,
points,  has
has  points and
points and  has
has 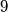 points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
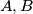 and
and  play a game with three cards and on each of these
play a game with three cards and on each of these  cards it is written a positive integer, all
cards it is written a positive integer, all  numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number
numbers are different. A game consists of shuffling the cards, giving each player a card and each player is attributed a number of points equal to the number written on the card and then they give the cards back. After a number 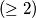 of games we find out that A has
of games we find out that A has 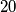 points,
points,  has
has  points and
points and  has
has 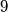 points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).
points. We also know that in the last game B had the card with the biggest number. Who had in the first game the card with the second value (this means the middle card concerning its value).  Školjka
Školjka  and all situated in the same semi-plane determined by a straight line which goes through
and all situated in the same semi-plane determined by a straight line which goes through 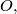 is at least 1.
is at least 1.  and
and  are natural numbers so that
are natural numbers so that 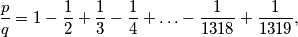 prove that
prove that 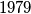 .
. 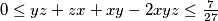 , where
, where 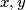 and
and  are non-negative real numbers satisfying
are non-negative real numbers satisfying 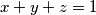 .
.  be any positive integer not equal to
be any positive integer not equal to 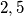 or
or 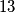 . Show that one can find distinct
. Show that one can find distinct 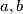 in the set
in the set 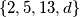 such that
such that 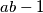 is not a perfect square.
is not a perfect square. 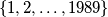 can be expressed as the disjoint union of subsets
can be expressed as the disjoint union of subsets 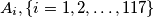 such that
such that 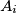 contains 17 elements
contains 17 elements