Consider the two square matrices
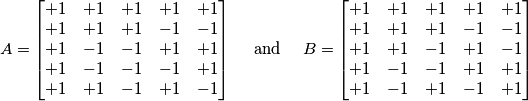
with entries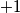 and
and  . The following operations will be called elementary:
. The following operations will be called elementary:
(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations.
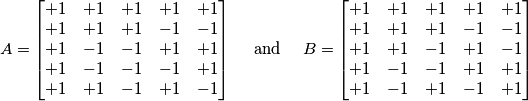
with entries
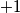 and
and  . The following operations will be called elementary:
. The following operations will be called elementary:(1) Changing signs of all numbers in one row;
(2) Changing signs of all numbers in one column;
(3) Interchanging two rows (two rows exchange their positions);
(4) Interchanging two columns.
Prove that the matrix
 cannot be obtained from the matrix
cannot be obtained from the matrix  using these operations.
using these operations.  Školjka
Školjka