Let
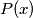
be a polynomial with integer coefficients. We denote
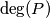
its degree which is
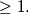
Let
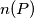
be the number of all the integers
for which we have
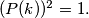
Prove that
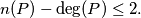
%V0
Let $P(x)$ be a polynomial with integer coefficients. We denote $\deg(P)$ its degree which is $\geq 1.$ Let $n(P)$ be the number of all the integers $k$ for which we have $(P(k))^{2}=1.$ Prove that $n(P)- \deg(P) \leq 2.$
Školjka