Let
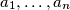
be an infinite sequence of strictly positive integers, so that
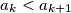
for any
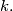
Prove that there exists an infinity of terms
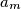
, which can be written like
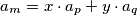
with
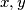
strictly positive integers and
.
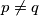
%V0
Let $a_{1}, \ldots, a_{n}$ be an infinite sequence of strictly positive integers, so that $a_{k} < a_{k+1}$ for any $k.$ Prove that there exists an infinity of terms $a_m$, which can be written like $a_m = x \cdot a_p + y \cdot a_q$ with $x,y$ strictly positive integers and $p \neq q$.
Školjka