IMO Shortlist 1991 problem 12
Dodao/la:
arhiva2. travnja 2012. Given any integer
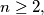
assume that the integers
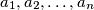
are not divisible by

and, moreover, that

does not divide
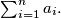
Prove that there exist at least

different sequences
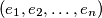
consisting of zeros or ones such
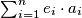
is divisible by
%V0
Given any integer $n \geq 2,$ assume that the integers $a_1, a_2, \ldots, a_n$ are not divisible by $n$ and, moreover, that $n$ does not divide $\sum^n_{i=1} a_i.$ Prove that there exist at least $n$ different sequences $(e_1, e_2, \ldots, e_n)$ consisting of zeros or ones such $\sum^n_{i=1} e_i \cdot a_i$ is divisible by $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991