Let
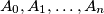
be points in a plane such that
(i)
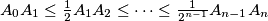
and
(ii)
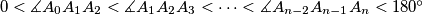
,
where all these angles have the same orientation. Prove that the segments
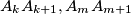
do not intersect for each

and

such that
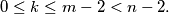
%V0
Let $A_0,A_1, \ldots , A_n$ be points in a plane such that
(i) $A_0A_1 \leq \frac{1}{ 2} A_1A_2 \leq \cdots \leq \frac{1}{2^{n-1} } A_{n-1}A_n$ and
(ii) $0 < \measuredangle A_{0}A_{1}A_{2} < \measuredangle A_{1}A_{2}A_{3} < \cdots < \measuredangle A_{n-2}A_{n-1}A_{n} < 180^\circ$,
where all these angles have the same orientation. Prove that the segments $A_kA_{k+1},A_mA_{m+1}$ do not intersect for each $k$ and $n$ such that $0 \leq k \leq m - 2 < n- 2.$