A sequence
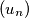
is defined by
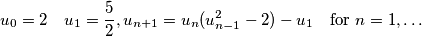
Prove that for any positive integer

we have
![[u_{n}]=2^{\frac{(2^{n}-(-1)^{n})}{3}}](/media/m/0/a/f/0afc47b8329bee70b003a95254582787.png)
(where {{ Nevaljan tag "x" }} denotes the smallest integer

x)

%V0
A sequence $(u_{n})$ is defined by $$u_{0}=2 \quad u_{1}=\frac{5}{2}, u_{n+1}=u_{n}(u_{n-1}^{2}-2)-u_{1} \quad \textnormal{for } n=1,\ldots$$ Prove that for any positive integer $n$ we have $$[u_{n}]=2^{\frac{(2^{n}-(-1)^{n})}{3}}$$(where [x] denotes the smallest integer $\leq$ x)$.$