Slični zadaci
For each positive integer  , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 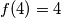 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
Prove that, for any integer we have
we have 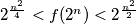 .
.
 , let
, let  denote the number of ways of representing
denote the number of ways of representing  as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance,
as a sum of powers of 2 with nonnegative integer exponents. Representations which differ only in the ordering of their summands are considered to be the same. For instance, 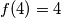 , because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1.
, because the number 4 can be represented in the following four ways: 4; 2+2; 2+1+1; 1+1+1+1. Prove that, for any integer
 we have
we have 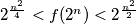 .
. Five students 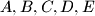 took part in a contest. One prediction was that the contestants would finish in the order
took part in a contest. One prediction was that the contestants would finish in the order 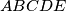 . This prediction was very poor. In fact, no contestant finished in the position predicted, and no two contestants predicted to finish consecutively actually did so. A second prediction had the contestants finishing in the order
. This prediction was very poor. In fact, no contestant finished in the position predicted, and no two contestants predicted to finish consecutively actually did so. A second prediction had the contestants finishing in the order 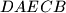 . This prediction was better. Exactly two of the contestants finished in the places predicted, and two disjoint pairs of students predicted to finish consecutively actually did so. Determine the order in which the contestants finished.
. This prediction was better. Exactly two of the contestants finished in the places predicted, and two disjoint pairs of students predicted to finish consecutively actually did so. Determine the order in which the contestants finished.
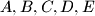 took part in a contest. One prediction was that the contestants would finish in the order
took part in a contest. One prediction was that the contestants would finish in the order 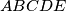 . This prediction was very poor. In fact, no contestant finished in the position predicted, and no two contestants predicted to finish consecutively actually did so. A second prediction had the contestants finishing in the order
. This prediction was very poor. In fact, no contestant finished in the position predicted, and no two contestants predicted to finish consecutively actually did so. A second prediction had the contestants finishing in the order 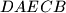 . This prediction was better. Exactly two of the contestants finished in the places predicted, and two disjoint pairs of students predicted to finish consecutively actually did so. Determine the order in which the contestants finished.
. This prediction was better. Exactly two of the contestants finished in the places predicted, and two disjoint pairs of students predicted to finish consecutively actually did so. Determine the order in which the contestants finished.  Školjka
Školjka 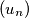 is defined by
is defined by 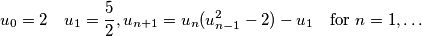 Prove that for any positive integer
Prove that for any positive integer ![[u_{n}]=2^{\frac{(2^{n}-(-1)^{n})}{3}}](/media/m/0/a/f/0afc47b8329bee70b003a95254582787.png) (where {{ Nevaljan tag "x" }} denotes the smallest integer
(where {{ Nevaljan tag "x" }} denotes the smallest integer  x)
x)
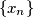 of positive reals such that
of positive reals such that 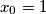 and
and 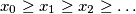 .
.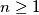 such that:
such that: 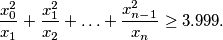
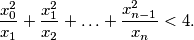
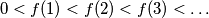 a sequence with all its terms positive
a sequence with all its terms positive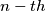 positive integer which doesn't belong to the sequence is
positive integer which doesn't belong to the sequence is 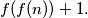 Find
Find 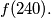
 be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length
be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length