Školjka A box whose shape is a parallelepiped can be completely filled with cubes of side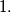 
If we put in it the maximum possible number of cubes, each ofvolume, 
, with the sides parallel to those of the box, then exactly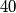 
percent from the volume of the box is occupied. Determine the possible dimensions of the box.
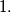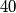If we put in it the maximum possible number of cubes, each ofvolume, , with the sides parallel to those of the box, then exactly percent from the volume of the box is occupied. Determine the possible dimensions of the box.