IMO Shortlist 1970 problem 10
Dodao/la:
arhiva2. travnja 2012. The real numbers
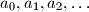
satisfy
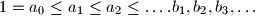
are defined by
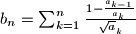
.
a.) Prove that
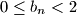
.
b.) Given

satisfying
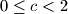
, prove that we can find

so that
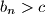
for all sufficiently large

.
%V0
The real numbers $a_0,a_1,a_2,\ldots$ satisfy $1=a_0\le a_1\le a_2\le\ldots. b_1,b_2,b_3,\ldots$ are defined by $b_n=\sum_{k=1}^n{1-{a_{k-1}\over a_k}\over\sqrt a_k}$.
a.) Prove that $0\le b_n<2$.
b.) Given $c$ satisfying $0\le c<2$, prove that we can find $a_n$ so that $b_n>c$ for all sufficiently large $n$.
Izvor: Međunarodna matematička olimpijada, shortlist 1970