Two identically oriented equilateral triangles,
with center
and
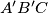
, are given in the plane. We also have
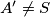
and
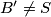
. If
is the midpoint of
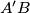
and
the midpoint of
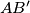
, prove that the triangles
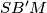
and
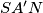
are similar.
%V0
Two identically oriented equilateral triangles, $ABC$ with center $S$ and $A'B'C$, are given in the plane. We also have $A' \neq S$ and $B' \neq S$. If $M$ is the midpoint of $A'B$ and $N$ the midpoint of $AB'$, prove that the triangles $SB'M$ and $SA'N$ are similar.
Školjka