We consider three distinct half-lines
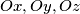
in a plane. Prove the existence and uniqueness of three points
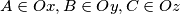
such that the perimeters of the triangles
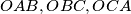
are all equal to a given number
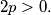
%V0
We consider three distinct half-lines $Ox, Oy, Oz$ in a plane. Prove the existence and uniqueness of three points $A \in Ox, B \in Oy, C \in Oz$ such that the perimeters of the triangles $OAB,OBC,OCA$ are all equal to a given number $2p > 0.$
Školjka