Odredi najveću vrijednost realne konstante
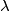
takve da za sve pozitivne realne brojeve

,

,

za koje je
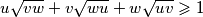
vrijedi nejednakost
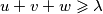
.
%V0
Odredi najveću vrijednost realne konstante $\lambda$ takve da za sve pozitivne realne brojeve $u$, $v$, $w$ za koje je $u\sqrt{vw} + v\sqrt{wu} + w\sqrt{uv} \geqslant 1$ vrijedi nejednakost $u + v + w \geqslant \lambda$.