Two circles in a plane intersect.  is one of the points of intersection. Starting simultaneously from
is one of the points of intersection. Starting simultaneously from  two points move with constant speed, each travelling along its own circle in the same sense. The two points return to
two points move with constant speed, each travelling along its own circle in the same sense. The two points return to  simultaneously after one revolution. Prove that there is a fixed point
simultaneously after one revolution. Prove that there is a fixed point  in the plane such that the two points are always equidistant from
in the plane such that the two points are always equidistant from 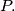
 is one of the points of intersection. Starting simultaneously from
is one of the points of intersection. Starting simultaneously from  two points move with constant speed, each travelling along its own circle in the same sense. The two points return to
two points move with constant speed, each travelling along its own circle in the same sense. The two points return to  simultaneously after one revolution. Prove that there is a fixed point
simultaneously after one revolution. Prove that there is a fixed point  in the plane such that the two points are always equidistant from
in the plane such that the two points are always equidistant from 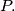
 Školjka
Školjka