IMO Shortlist 1988 problem 18
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Consider 2 concentric circle radii  and
and  (
(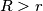 ) with centre
) with centre 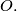 Fix
Fix  on the small circle and consider the variable chord
on the small circle and consider the variable chord 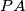 of the small circle. Points
of the small circle. Points  and
and  lie on the large circle;
lie on the large circle; 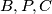 are collinear and
are collinear and  is perpendicular to
is perpendicular to 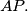
i.) For which values of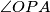 is the sum
is the sum 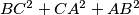 extremal?
extremal?
ii.) What are the possible positions of the midpoints of
of 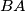 and
and  of
of  as
as 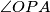 varies?
varies?
 and
and  (
(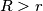 ) with centre
) with centre 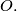 Fix
Fix  on the small circle and consider the variable chord
on the small circle and consider the variable chord 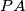 of the small circle. Points
of the small circle. Points  and
and  lie on the large circle;
lie on the large circle; 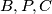 are collinear and
are collinear and  is perpendicular to
is perpendicular to 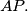
i.) For which values of
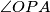 is the sum
is the sum 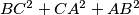 extremal?
extremal? ii.) What are the possible positions of the midpoints
 of
of 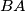 and
and  of
of  as
as 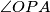 varies?
varies? Izvor: Međunarodna matematička olimpijada, shortlist 1988
 Školjka
Školjka 
