Let

be the number of integral solutions of the equation
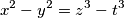
satisfying the condition
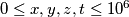
, and let

be the number of integral solutions of the equation
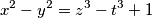
satisfying the condition
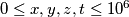
. Prove that
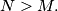
%V0
Let $N$ be the number of integral solutions of the equation
$$x^2 - y^2 = z^3 - t^3$$
satisfying the condition $0 \leq x, y, z, t \leq 10^6$, and let $M$ be the number of integral solutions of the equation
$$x^2 - y^2 = z^3 - t^3 + 1$$
satisfying the condition $0 \leq x, y, z, t \leq 10^6$. Prove that $N >M.$