Let
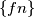
be the Fibonacci sequence
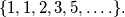
(a) Find all pairs
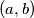
of real numbers such that for each

,
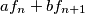
is a member of the sequence.
(b) Find all pairs
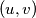
of positive real numbers such that for each

,
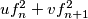
is a member of the sequence.
%V0
Let $\{fn\}$ be the Fibonacci sequence $\{1, 1, 2, 3, 5, \dots.\}.$
(a) Find all pairs $(a, b)$ of real numbers such that for each $n$, $af_n +bf_{n+1}$ is a member of the sequence.
(b) Find all pairs $(u, v)$ of positive real numbers such that for each $n$, $uf_n^2 +vf_{n+1}^2$ is a member of the sequence.