Find the minimum value of
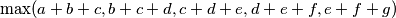
subject to the constraints
(i)
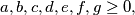
(ii)
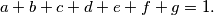
%V0
Find the minimum value of
$$\max(a + b + c, b + c + d, c + d + e, d + e + f, e + f + g)$$
subject to the constraints
(i) $a, b, c, d, e, f, g \geq 0,$
(ii)$a + b + c + d + e + f + g = 1.$