Let

be a convex polygon in the plane and suppose that

is positioned in the coordinate system in such a way that
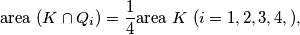
where the
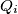
denote the quadrants of the plane. Prove that if

contains no nonzero lattice point, then the area of

is less than
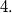
%V0
Let $K$ be a convex polygon in the plane and suppose that $K$ is positioned in the coordinate system in such a way that
$$\text{area } (K \cap Q_i) =\frac 14 \text{area } K \ (i = 1, 2, 3, 4, ),$$
where the $Q_i$ denote the quadrants of the plane. Prove that if $K$ contains no nonzero lattice point, then the area of $K$ is less than $4.$